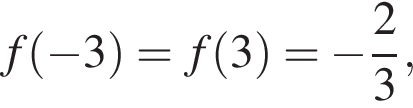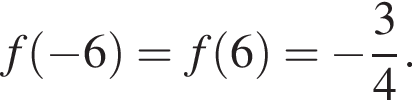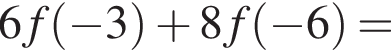1. Задание № 182 

Сложность: I
Классификатор алгебры: Симметрия относительно точки и прямой
Симметрия относительно точки и прямой
i
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.
1) 1
2) 2
3) 3
4) 4
5) 5
Решение. Симметрия относительно прямой (или осевая симметрия) — это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону прямой, всегда будет соответствовать точка, расположенная по другую сторону прямой, а отрезки, соединяющие эти точки, будут перпендикулярны оси симметрии и делятся ею пополам.
Фигуры, симметричные относительно прямой l, изображены на рисунке 2.
Правильный ответ указан под номером 2.
Ответ: 2
182
2
Сложность: I
Классификатор алгебры: Симметрия относительно точки и прямой
 Тогда длина BX равна
Тогда длина BX равна 
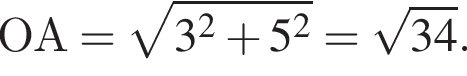
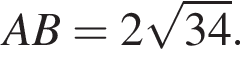
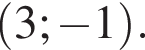
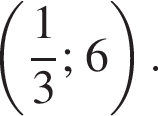 Значение выражения k + b равно:
Значение выражения k + b равно: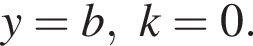 Прямая проходит через точку A с координатами
Прямая проходит через точку A с координатами 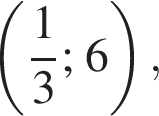 отсюда b = 6. Поэтому k + b = 6.
отсюда b = 6. Поэтому k + b = 6.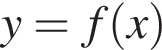 определена на множестве действительных чисел, точки
определена на множестве действительных чисел, точки 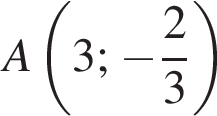 и
и 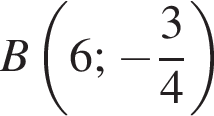 принадлежат графику данной функции. Найдите значение выражения
принадлежат графику данной функции. Найдите значение выражения  если известно, что график функции
если известно, что график функции